Improved Fat/Water Reconstruction Algorithm with Graphics Hardware Acceleration
David H. Johnson, Chris A. Flask, Sreenath Narayan, and David L. Wilson
This is an author's electronic pre-print of the following publication. JMRI allows pre-prints to be shared through individual author's websites; for terms, please see this website's license. Please cite the published work as:
Improved fat-water reconstruction algorithm with graphics hardware acceleration. Free HTML format! Johnson DH, Narayan S, Flask CA, Wilson DL. J Magn Reson Imaging 2010;31(2):457-465. Pubmed: 20099358. Journal's version: 10.1002/jmri.22051.
Address for correspondence: David L. Wilson, Ph.D. dlw@case.edu.
ABSTRACT
Purpose. To develop a fast and robust Iterative Decomposition of water and fat with Echo Asymmetry and Least-squares (IDEAL) reconstruction algorithm utilizing graphics processor unit (GPU) computation.
Materials and Methods. The fat-water reconstruction was expedited by vectorizing the fat-water parameter estimation, which was implemented on a graphics card to evaluate potential speed increases due to data-parallelization. In addition, we vectorized and compared Brent's method to golden section search for the optimization of the unknown field inhomogeneity parameter (ψ) in the IDEAL equations. The algorithm was made more robust to fat-water ambiguities using a modified planar extrapolation (MPE) of ψ algorithm. As compared to simple planar extrapolation (PE), the use of an averaging filter in MPE made the reconstruction more robust to neighborhoods poorly fit by a 2D plane.
Results. Fat-water reconstruction time was reduced by up to a factor of 11.6 on a GPU as compared to CPU-only reconstruction. The MPE algorithms incorrectly assigned fewer pixels than PE as using careful manual correction as a gold standard (0.7% vs. 4.5%, P<10-4). Brent's method used fewer iterations than golden section search in the vast majority of pixels (6.8±1.5 vs. 9.6±1.6 iterations).
Conclusion. Data sets acquired on a high field scanner can be quickly and robustly reconstructed using our algorithm. A GPU implementation results in significant time savings, which will become increasingly important with the trend towards high resolution mouse and human imaging.
Keywords: IDEAL, Graphics cards, GPU, fat-water estimation, image reconstruction.
INTRODUCTION
Iterative Decomposition and Echo Asymmetry with Least squares estimation (IDEAL) (1) is a robust fat-water reconstruction technique, but it can be computationally expensive. At our institution we are developing a comprehensive program for MR imaging of mouse models of obesity and metabolic disorders so as to determine the role of genes, diet, activity, and drugs on this important health problem. We are developing methods to characterize lipid accumulation in various fat depots including visceral and subcutaneous adipose tissue, as well as ectopic depots in muscle and liver. Prior to herein described improvements, whole mouse scans on our high field scanners consisted of over 150 MB, with the time for processing and manual correction exceeding 1 hour, greatly exceeding the acquisition time of 15 min. Planned improvements in data acquisition will generate higher resolution data and increased animal throughput, creating a significant data analysis bottleneck. In addition, if one were to acquire IDEAL-type data at today’s resolution for whole human scans (2), data size (>600 MB), the time for processing would be very daunting.
The IDEAL reconstruction algorithm is fundamentally the same in each pixel, which implies that the operations can be carried out in parallel. This type of data-parallel reconstruction is appropriate for using a highly parallel, graphics processor unit (GPU). The Nvidia CUDA architecture makes it possible to realize highly parallel algorithms on commodity graphics cards (Fig 1). Other MRI reconstruction algorithms, e.g. SENSE, have recently been shown to be much faster when implemented on graphics hardware (3). We investigated the potential speedups in the IDEAL reconstruction when using a GPU, and we made improvements to the reconstruction to make it more suitable for GPU implementation.
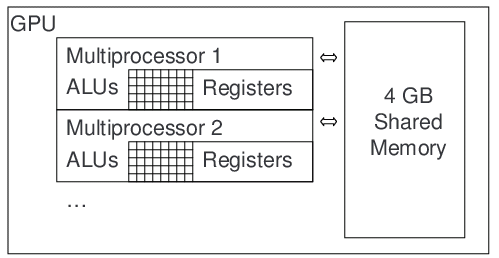
Figure 1. Nvidia CUDA architecture for massively parallel GPU computation. The Quadro FX5800 has 10 SIMT (Single Instruction, Multi-Threaded) multiprocessors, each of which has 24 scalar stream processors running at 400 MHz. Thousands of threads can be simultaneously executed on the multiprocessors, which have a 102 GB/s connection to shared memory. IDEAL is well-suited to SIMT computation because the mathematical operations for reconstruction are identical in each pixel, and the large IDEAL image sets can be stored in the shared memory.
In the present report, we first describe algorithms including vectorized IDEAL equations as well as vectorized versions of Brent’s method (4) and golden section search (5) for optimizing the field inhomogeneity parameter (Ψ). We also improve the planar extrapolation algorithm to be more robust to fat-water ambiguities and ψ aliasing errors. In Results, we compare results to those obtained following careful manual editing within our GUI program. We also compare computation time as a function of data size and algorithm. Finally, we discuss time savings and accuracy improvements of our methods and generalize to other computational configurations.
THEORY
The IDEAL reconstruction method has been published in detail elsewhere (1). Here we focus on the vectorization modifications needed to enable massively parallel computation. The real and imaginary components of the MRI signal (S) in a voxel can be modeled as a function of the echo time (TE), fat-water frequency difference (Δf), the field inhomogeneity in Hz (ψ), and the fat and water components (pW and pF) in Eq. 1.
(1)
If the signal is acquired at multiple echo times (e.g., TE1, TE2, TE3) then a system of equations can be used to describe the observed signals S(TE1), S(TE2), and S(TE3). The system can be compactly represented as a product of matrices as per Eq. 2.
(2)
The observed signals can then be fit in a least squares sense by finding the value of ψ which minimizes the differences between the observed signals and the values predicted by the right hand side of Eq. 2. A substitution for the observation matrix (A) indicated in Eq. 2 eases the notation which follows. The pseudo inverse of the observation matrix (A†) is given by where H denotes the Hermetian transpose. The sum of squared differences (i.e. the residuals, J) can be found as a function of ψ by the matrix multiplications indicated in Eq. 3, which is the variable projection (VARPRO) formulation of IDEAL (6).
(3)
As described by Reeder, ψ may be initialized to zero in every pixel (7). The residuals are then reduced by iteratively trying new estimates of ψ. When a value of ψ which minimizes the residuals is found in a given pixel, the fat and water components are determined in a least squares sense as per Eq. 3. The optimization of Eq. 3 and evaluation of Eq. 4 must be repeated in every pixel of the image. The optimal ψ can be found by a line search algorithm such as gradient descent, golden section search, or Brent's method.
(4)
There is a fundamental ambiguity in IDEAL reconstruction which necessitates the use of spatial smoothness constraints to find the correct solution for ψ in each pixel. There are usually two local minima in the residuals, and these two solutions simply “flip” the numerical results for fat and water density (8). In general, there will be two possible solutions (ψW, ψF) corresponding to assigning the dominant component to water and the minor component to fat, or vice versa. Given one value, the "flipped" value of ψ can be computed (5). There is a degenerate case where the both components are exactly equal and only one solution for ψ exists, but this case is very rare in vivo and will not be considered further here. Replicas of the two solutions occur at predictable 1/ΔTE intervals, also called ψ aliasing (5). Although this ambiguity problem seems insurmountable, it is not because ψ varies smoothly in space. The best solution in a given pixel can be found by using neighboring pixels to predict which the solution among the replicates of ψW, ψF is the smoothest (i.e. the minimum absolute difference between the predicted ψ and the replicated local minima).
Spatial smoothness over a neighborhood of pixels can be modeled in several ways. Planar Extrapolation (PE) (8), is one technique for finding the correct value of ψ in each pixel. The correct value of ψ is assumed to be known in a seed pixel, determined either manually or automatically, and planar extrapolation from the solved portion of the image is used to pick the smoothest solution in each subsequent pixel in a region growing operation. The planar model for ψ over a local neighborhood is formulated in a least squares sense from currently fitted pixels. The parameters of the plane include a slope along each axis (ψx, ψy) and an average value (ψ0) given by Eq. 5.
(5)
Given a neighborhood of solved pixels at pixel coordinates (x(1),y(1), x(2),y(2),…) with known fat-water solutions (ψ(1), ψ(2)…), the parameters of the plane are fitted in a least squares sense by Eq. 6.
(6)
After fitting the parameters of the plane, the predicted value of ψ at the current (x,y) coordinates can then be evaluated using Eq. 5. Air pixels and other regions with no signal are not allowed to influence fitting the parameters of the plane by weighting each pixel in Eq. 6 by the magnitude of the signal at the first echo time (8).
To improve robustness of the PE technique, we created a modified planar extrapolation (MPE) algorithm having multiple enhancements. As shown later, these modifications are necessary to produce robust and accurate Psi maps in T1-weighted images. First, the weighting is made binary. That is, all non-air pixels are weighted equally. All non-air pixels should give the same weight to the extrapolation because each non-air pixel contains the same amount of new information about ψ. Violating this condition causes extrapolation errors because fat pixels do not actually contain more information about ψ.
The second enhancement in MPE is an a priori constraint applied to fitting the parameters of the plane. Local variations in SNR (i.e., near cardiac or respiratory motion) may cause physically unrealistic least squares fits. Therefore, the slope of each axis should not be greater than 2/ΔTE/N, where N is the number of pixels on the axis. If the fitted parameters of the plane do not satisfy this requirement then planar extrapolation is inappropriate in this region of the image. The fitted plane is rejected, and the neighborhood is refitted using the mean value of ψ in the neighborhood (i.e. the sum of the ψ values in the neighborhood divided by the number of the pixels in the neighborhood). This is equivalent to an averaging filter, which is less sensitive to local variations in SNR and therefore far less likely to produce unrealistic fitting of ψ.
Vectorization of IDEAL. The entire image can be reconstructed simultaneously by vectorizing Eqs. 3-4, which enables efficient GPU computation. The observation matrix is not a function of the pixel coordinates. Therefore Eq. 3 can be rewritten as a matrix product when a temporary matrix T is used, as per Eq. 7. Note that the '*' operator has been introduced to indicate a per-element multiplication instead of a standard matrix inner product. Each column of the matrices in Eq. 7 corresponds to the observed signals in the pixel at the index x, where x varies from 1 to the number of pixels in the image.
(7)
Computation of the residuals is then vectorized in Eq. 8, where one column again corresponds to evaluating the residuals in each pixel. Different values of Ψ are then iteratively evaluated in each pixel of the image until all the pixels of the image are solved.
(8)
The final evaluation of the fat and water components is also vectorized, as per Eq. 9.
(9)
Equations 7-9 are easily implemented on a GPU using matrix operations. The vectorized IDEAL algorithm is very efficient (i.e. high arithmetic density per data point). As with the scalar case, the optimal Ψ can be found by a line search algorithm evaluated in each pixel. Next, we describe how golden section search and Brent's method can both be vectorized on a GPU.
Golden section search can be used to find local minima in the residuals as a function of ψ, which corresponds to finding ψW or ψF (5). By definition, a minimum near ψ=b is bracketed by the bounds (a and c) if the residuals (J) fulfill the following relationships: a<b<c and J(a)>J(b) and J(c)>J(b) (4). A trial point is tested at ψ=d where splits the intervals (b,d) and (d,c) into the golden ratio (1+√5)/2. If J(d)<J(b) the outside bracket is updated to the (b,c) interval, and a new trial point is generated that splits the (b,d) interval by the golden ratio. If J(d)>J(b), the (a,b) interval will instead be split and evaluated, and the outside bracket is updated to the (a,d) interval. This process is recursively repeated until the width of the bracket is reduced to an acceptable error (e.g. (a-c)<1 Hz). The solution for ψ is returned as the smallest of the function values most recently evaluated.
Vectorization of golden section search is straightforward because the intervals can be turned into column vectors with one entry in the vector for each pixel being solved. Operations on a, b, c, and d can be performed with vector math and logical indexing. For example, the test of J(d)<J(b) can be accomplished with a per-element comparison, and indices of the elements where the test was true are used to split the (a,b) interval.
Brent's method combines inverse quadratic interpolation with golden section search because the former has quadratic convergence, whereas the latter has only linear convergence (4). Brent's method uses a parabolic fit to "jump" to the solution with many fewer iterations than golden section search. The minimum x value (apex) of the parabola passing through the points (X, J(X)), (V, J(V)), and (W,J(W)) is given by:
(10)
Brent's method can be summarized as follows. Like golden section search, the minimum near ψ=b is bracketed by the bounds (a and c). Brent's method fits a parabola between the best three points most recently evaluated (x,v,w) as well as the value of the residuals at these points (fx,fv,fw). Parabolic interpolation is attempted according to Eq. 10 to generate a trial point at the apex. The residuals are evaluated at the trial point unless it lies outside the (a,c) interval or it is too close to either endpoint or it is too close to a point on the last or second to last evaluation. If predicted apex is rejected, the golden section step is taken instead as defined above by golden section search. Regardless of which method is used to generate the trial point, the outside interval (a,c) is updated at each iteration to shrink the interval of uncertainty until the desired error tolerance is achieved.
Brent's method is more complicated to vectorize than golden section search because of the additional tests used to constrain the parabolic interpolation, but the basic ideas remain the same. All of the internal variables of the algorithm are replaced by column vectors, and logical indexing is used in place of the tests for being too close to endpoints or recently evaluated points. Parabolic interpolation is used whenever allowed by the above criteria, and convergence is guaranteed by the slow but reliable golden section steps when parabolic interpolation fails.
METHODS
MRI Acquisitions. High resolution shifted spin echo scans were acquired on a Bruker Biospec 7T/30cm of 26 week old C57BL/6J male mice on a high fat diet mice (N=6) or a low fat diet (N=6) (Jackson Laboratory Diet-Induced Obesity Service, D12492i 60 kcal% fat chow vs. D12450Bi, 10 kcal% fat chow, Research Diets, Inc.). A T1-weighted Rapid Acquisition with Relaxation Enhancement (RARE) sequence with varying echo asymmetry delays was used to achieve p/6, 5p/6, and 3p/2 radian shifts between fat and water (TR=1087 ms/gated, TE=9.1 ms, 102 x 40 to 102 x 50 mm FOV, 512x256 matrix, 4 averages, and echo asymmetry delays of 79, 396, and 714 us). Animal studies were conducted under an approved animal protocol.
GPU Implementation. Algorithms were implemented on a desktop computer with 32GB RAM, dual Intel Xeon X5450 3.0 GHz processors, an Nvidia Quadro FX5800 (4GB RAM, 240 cores, 400 MHz clock), and Matlab R2009a 64bit with Accelereyes Jacket v1.1. Jacket is a library that enables GPU computations within Matlab using Nvidia CUDA.
Computational Evaluations. To evaluate computation times for GPU and CPU implementations, we performed reconstruction tests with different image sizes. A 512x256 mouse image with 3 TEs was reconstructed using Eqs. 7 and 9 with 100 fixed values of ψ in each pixel to test the execution time of the GPU and CPU implementations. The image was logarithmically resampled to determine how the GPU and execution times varied with the number of pixels. Execution time was recorded for eleven repetitions of the reconstruction test, and the first repetition was discarded. The remaining repetitions were averaged. Additionally, a CPU-only test was performed by changing the number of concurrent threads allowed in Matlab and repeating the reconstructions to determine how much benefit could be derived from using the multiple CPU cores. The number of threads was limited to eight, one per processor core. Eleven repetitions were recorded and all but the first were averaged. To compare numbers of iterations for golden section search and Brent's method, we started both routines with the same initial condition (ψ=0) and recorded the number of iterations needed to isolate minima of residuals. To illustrate the advantage of parabolic interpolation in finding the minimum, signals of one pixel at 3 TEs were extracted from the mouse dataset in a pixel inside the spinal muscles (i.e. near the center of the FOV and known to be dominantly water). One function evaluation was allowed per iteration of the optimization routine. Iteration was stopped when ψ changed by less than 0.1 Hz. The test was repeated in all pixels of a 512x256 test image, and histograms of the number of iterations used by each algorithm was created.
Manual Correction Software. A custom user interface for manually editing ψ maps was created in Matlab. After loading the image data and identifying the two possible solutions in each pixel, the solution assigning water to the dominant component (ψW) was assigned to all pixels. Several image operations were then used to find the correct solution for ψ in the image. The operator initializes either PE or MPE manually by clicking the image, and the operator can use a 20x20 median filter on the ψ image to switch between the two possible solutions by reassigning each pixel to the minimum absolute difference between the median of the neighborhood and the possible solutions (i.e. ψW, ψF and the 1/ΔTE replicates). The size of the median filter can be adjusted. The median filter operation is entirely sufficient to solve many images because there is often more water than fat in the image, or the fat regions are smaller than the water regions so the median filter will propagate the correct solution into the fat regions. Locally incorrect yet smooth regions may remain in some images, which are solved by clicking on the ψ map to initialize a local region growing operation. The mean (μψ) and standard deviation (σψ) of ψ values in the 3x3 neighborhood around the mouse click are calculated, and then the region growing operation originates at the mouse click and continues outward, stopping at thresholds of ψ=μψ±K*σψ, where K is a user-controlled scalar (e.g. 0.1 to 10).
Evaluation of Accuracy. To compare the accuracy of the PE and MPE algorithms, we compared the fat and water reconstructions of each algorithm to ground truth data in a total of 236 images in 12 mouse datasets. Ground truth results were created manually by an experienced operator using our editing software. The ground truth ψ map was compared to the output of the MPE and PE algorithms. The number of non-air pixels where fat and water were flipped was counted for each algorithm. Air pixels were excluded by applying a threshold to the original magnitude image of μair+3*σair, where the mean (μair) and standard deviation (σair) of air intensity was automatically determined from the 10x10 pixels in the upper left hand corner of the image. We determined the dependence of PE and MPE processing on algorithm parameters by repeating runs on images using the same seed point. For PE and MPE, we evaluated window sizes of 20x20, 25x25, and 30x30 pixels. MPE used with a 25x25 pixel window and limiting ψx and ψy to 15 Hz/pixel.
RESULTS
The MPE algorithm was much more successful than the PE algorithm. The robustness of fitting ψ was improved by both binary weighting (i.e. masking) and an a priori constraint applied to fitting the parameters of the plane. For masking, all non-air pixels are weighted equally. The alternative of using the magnitude of the signal as a non-binary weight is problematic because more extrapolation weight will be given to hyper-intense fat pixels than to water pixels. This latter alternative results in errors in neighborhoods containing both fat and water (Fig 2-a). Instead of using the magnitude of the signal at the first echo time (Fig 2-b, c, and d), the weight is set to 1 if the magnitude of the signal at the first echo time is greater than an a priori threshold and 0 otherwise (Fig 2-e, f, and g). Masking prevents extrapolation errors in this region (Fig 2-d vs. g).
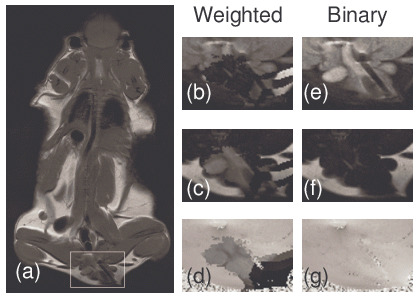
Figure 2.All non-air pixels should give the same weight to the extrapolation and fitting of ψ because each non-air pixel contains the same amount of new information about local field inhomogeneities. Extrapolation errors occur in the boxed region of (a) when signal weighting is used (magnified images (b)-(d), containing the erroneous water, fat, and psi estimates, respectively). Therefore, a tissue mask (weight=1 in all non-air voxels, weight=0 in air voxels) is used instead. In contrast to signal weighting which failed in this region, masking prevents the extrapolation errors, (d)-(g), correct water, fat, and psi estimates, respectively.
MPE was also enhanced by utilizing a priori constraints on the fitting the parameters of the plane. In Fig 3, the initial ψ image contained ψ aliases of +3150 Hz and -3150 Hz near the top and bottom of the image. PE failed in these regions and caused errors of over 3150 Hz to propagate past the lungs and intestines even when different window sizes were used (Fig 3-c, d, and e). MPE was able to successfully solve this image (Fig 3-f), giving <1% error pixels. These are typical results among many other image slices. Multiple seed points were used to attempt to fix the PE results, but all failed with similar errors (images not shown). In contrast, the MPE method was relatively insensitive to the choice of seed point.


Figure 3. Comparison of the planar extrapolation (PE) and the modified planar extrapolation (MPE) algorithms. The reference magnitude image (a) and initial ψ map with many errors (b) are shown. When PE is performed with a variety of window sizes, 20x20, 25x25, and 30x30 (c-e, respectively), errors result when the window passes through the lungs and/or intestines. In comparison, MPE with a 25x25 window (f) does not suffer from these artifacts and finds a high quality ψ map. Those few remaining irregularities in ψ tend to occur in the lungs or the heart where fat-water calculations are corrupted by motion. The tissue mask (g) shows air pixels (black, weight=0) and non-air pixels (white, weight=1).
MPE performed significantly better (P<10-4) than the standard PE algorithm, as determined a Wilcoxon-rank-sum test of the number of incorrectly assigned pixels in a study of 236 images in 12 mouse datasets (Fig 4). The error rate of the proposed method was six times lower than the standard extrapolation routine (0.7% vs. 4.5% of incorrectly assigned pixels normalized to the total number of non-air pixels). PE had no errors in 92 out of the 236 images, as compared to 167 images for MPE. Most of the errors after MPE were due to respiratory motion. As described previously, these remaining errors were corrected manually, which never required more than a minute for each dataset. Less time was spent on manual corrections using MPE than PE because fewer errors occurred.
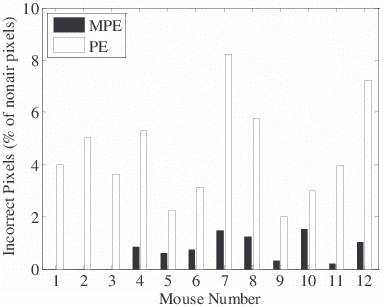
Figure 3. Comparison of number of pixels erroneously assigned (fat as water or vice versa) among a study of six low fat diet mice (mice 1-6) and high fat diet mice (7-12). A total of 236 images were processed by both algorithms and results were compared to the same images processed with careful manual editing. Air pixels were excluded by applying a threshold to the magnitude image. The number of pixels incorrectly assigned by MPE is significantly lower than PE (P < 10-4).
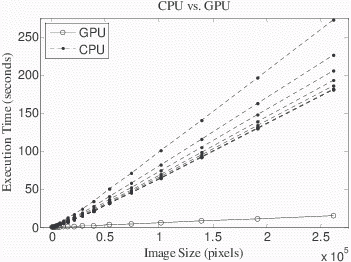
The GPU implementation was ~10X faster than the CPU-only implementation for 512x256 images (8.6±0.2 vs. 92.0±0.3 s, mean ± 1 s.d., P<0.01, Fig 5-a). The CPU-only test with multithreading showed that images all sizes were faster using more threads, but there was less improvement with an increasing number of cores utilized (Fig 5-a, dashed lines). Utilizing up to 4 cores (i.e. 4 threads) reduced reconstruction time by 43% (98.7±0.3 vs. 141.1±0.4 s, P<0.01) but using the full 8 cores only provided another 7% reduction in execution time as compared to 4 cores (92.0±0.3 vs. 98.7±0.3 s, P<0.01). CPU mulithreading little affected reconstruction speed when the GPU was used (<1 s, data not shown).
a)

b)
Figure 5. GPU versus CPU processing time for IDEAL reconstruction. (a) GPU and CPU execution times are plotted as a function of image size for a 3 TE reconstruction (N=11 repetitions of the reconstruction, dropping the first and averaging the others). For images of all sizes, the GPU was faster than the CPU (P<0.01), and for a 512x256 image, execution time was ~10X faster on the GPU as compared to the CPU with 8 threads (8.6±0.2 vs. 92.0±0.3 s, mean ± 1 s.d., P<0.01). (b) The ratio of the CPU to GPU execution times was only 2.6 at the smallest image size tested (512 pixels) but the ratio increased to 11.6 for the largest image size tested (512x512 pixels). The ratio does not appear to increase further for larger images. Considering a very high resolution image of 2048x2048 (4.2 million pixels) with 3 TEs, the trend extrapolates to an execution time on 47.8 min on the CPU as compared to only 4.1 min on the GPU.
The GPU implementation was faster than the CPU for images of all sizes, and the advantage of the GPU improved with larger image sizes (Fig 5-b). Whereas the ratio of the CPU to GPU execution times was only 2.6 for the at the smallest image size tested (512 pixels), the ratio increased to 11.6 for the largest image size tested (261,888 pixels). The trajectory of the curves suggests that the speed advantage of the GPU will continue to improve over the CPU for larger images.
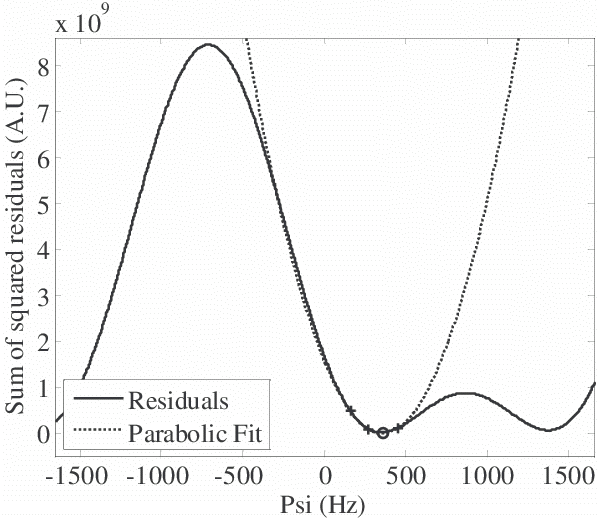
Figure 6. Brent’s method uses inverse quadratic interpolation to quickly find minima in the residuals vs. Ψ curve. The initial brackets (crosses, +) are used to fit a parabola and “jump” to the apex, which is near the minimum (circle). For the same initial conditions in this example, Brent’s method isolates the minimum in 7 iterations as compared to 13 iterations for golden section search.
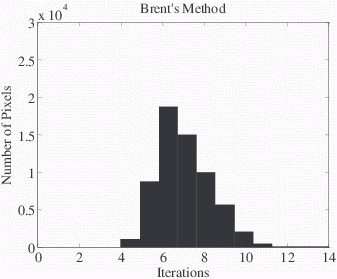
Brent's method required fewer iterations to isolate minima in ψ than golden section search (7 vs. 13 iterations, respectively, for the example in Fig 6). Over the non-air pixels in a 512x256 test image (shown in Fig 3-b), Brent’s method required fewer iterations than golden section search in over 93% of non-air pixels (6.8±1.5 vs. 9.6±1.6 iterations, P<0.01, Wilcoxon signed rank test, Fig 7). The center of the histograms of the number of iterations showed a reduction of 3 iterations for most pixels. Brent's method was actually approximately 10% slower than golden section search for the size of the images as originally acquired (512x256), but for a sufficiently large dataset (2048x2048) we extrapolated that it would have been faster.
a)

b)
Figure 7. Histograms of the number of iterations to solve the non-air pixels in a 512x256 test image (displayed in Fig 2) demonstrate that Brent’s method typically requires fewer iterations. Starting from the same initial conditions, the iterations required for each method to isolate the minima were recorded. Brent’s method required fewer iterations than golden section search in over 93% of non-air pixels (6.8±1.5 vs. 9.6±1.6 iterations, P<0.01 Wilcoxon signed rank test).
DISCUSSION
We determined multiple key features for creating a fast, robust IDEAL reconstruction method suitable for mouse imaging on a high field scanner with significant B0 field inhomogeneity. First, the vectorized IDEAL equations enabled the use of a massively parallel graphics card and multithreading on a multi-core CPU. Second, Brent's method was used to quickly find the correct solution of ψ when minimizing residuals, which reduced the number of iterations needed in the IDEAL reconstruction. Third, the planar extrapolation model was improved by limiting the fitted slopes of the extrapolation and switching to an averaging filter in the case of a bad fit, which robustly eliminated errors throughout the image.
Before the improvements described here utilizing the GPU, the MPE algorithm, and Brent's method, reconstruction time including manual corrections was exceeding acquisition time (1 hr. vs. 15 min.), and after implementing these changes we can routinely analyze large volumes of mouse data in under 5 min. per mouse dataset. The MPE algorithm enables higher animal throughput and decreases burden the burden of making manual corrections, which is critical for future research projects involving ultra-high resolution datasets. Extrapolation of the CPU and GPU trends of isolating minima (Fig 7) to an ultra-high resolution 2048x2048 dataset implies an execution time on 47.8 min on the CPU as compared to only 4.1 min on the GPU. This method can also be translated to clinical applications where post-processing time must be minimized. The current trend appears to be to 3T or even 7T human scanning, where B0 corrections and fast data processing will be needed. Clearly, GPU usage is critical for the future of high resolution, small animal and human imaging.
One limitation of the current results is that our implementation of Brent’s method was slightly slower than golden section search, despite the reduction in iterations being used in Brent’s method. For sufficiently large datasets Brent's method would be faster, but in the small datasets which can currently be acquired with in-vivo mouse image, golden section search is actually faster in our datasets. Each individual iteration of Brent’s method cannot be as fast as golden section search because Brent’s method must always perform more calculations (i.e. inverse parabolic interpolation) and keeps track of more data (the best three points most recently evaluated (x,v,w) as well as the value of the residuals at these points (fx,fv,fw)). However, Brent’s method is better than golden section search because it requires fewer evaluations of the residuals at each pixel, and we anticipate that improved GPU support for iterative algorithms might give a better result in the near future.
In this preliminary work, both PE and MPE were manually initialized from the same pixel. However, PE and MPE could also be initialized automatically using the center of mass algorithm (8). We evaluated MPE in a total of 236 images in 12 mouse datasets, and MPE gave consistently better results than PE regardless of initial condition. The automatic initialization of PE and MPE will be addressed in future work.
Further optimization can possibly be obtained by replacing Brent's method with alternatives. Implementing a vectorized version of Newton's method appears promising because analytical first and second derivatives with respect to ψ are available for Eq. 8. Newton's method typically has the fastest possible convergence among line search algorithms if the starting condition is close enough to the minimum though caveats remain about maintaining brackets and minimum step sizes. It remains to be seen if algebraic decomposition and harmonic retrieval (9) are faster than the proposed method because they involve much more computationally expensive mathematical operations (i.e. per-pixel singular value decomposition). However, algebraic decomposition cannot account for T2* decay, whereas the vectorized forms of Eq. 7-9 can model T2* decay without modification. Future work will include an optimization routine that estimates the imaginary component of ψ (i.e. T2* decay).
We considered replacing the “averaging filter” in the MPE algorithm with a median filter. A better result might be obtained with a 2D median filter because the median value of ψ is able to track smooth changes and ignore outliers more effectively than the linear filters. Unfortunately the median filter requires sorting, which is difficult to implement efficiently on a GPU. The 2D weighted averaging filter is sufficient to improve upon the planar extrapolation routine and avoid propagated errors in our images.
In conclusion, we developed a robust and time-efficient technique for reconstructing IDEAL fat and water images on a high field scanner. The speed of IDEAL reconstruction was increased by using Brent's method and graphics card processing. The accuracy of IDEAL reconstruction was improved by using a more robust planar extrapolation routine. These improvements will be critical for future studies of large numbers of mice with high resolution acquisitions and also of high resolution human imaging.
ACKNOWLEDGEMENTS
We thank the staff of our imaging center for assistance with animal handling.
References
1. S.B. Reeder, A.R. Pineda, Z. Wen, et al. Iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL): application with fast spin-echo imaging. Magn Reson Med 2005:54:636-644.
2. J. Machann, C. Thamer, B. Schnoedt, et al. Standardized assessment of whole body adipose tissue topography by MRI. J.Magn Reson.Imaging 2005:21:455-462.
3. M.S. Hansen, D. Atkinson, T.S. Sorensen. Cartesian SENSE and k-t SENSE reconstruction using commodity graphics hardware. Magn Reson Med 2008:59:463-468.
4. W.H. Press, S.K. Teukolsky, W.T. Vetterling, B.P. Flannery. Minimization or Maximization of Functions. In: W. H. Press, S. K. Teukolsky, W. T. Vetterling, and B. P. Flannery (Eds.), editors. Numerical Recipes in C: the Art of Scientific Computing. Cambridge: Cambridge University Press; 1992. pp. 394-455.
5. W. Lu, B.A. Hargreaves. Multiresolution field map estimation using golden section search for water-fat separation. Magn Reson Med 2008:60:236-244.
6. D. Hernando, J.P. Haldar, B.P. Sutton, J. Ma, P. Kellman, Z.P. Liang. Joint estimation of water/fat images and field inhomogeneity map. Magn Reson.Med. 2008:59:571-580.
7. S.B. Reeder, Z. Wen, H. Yu, et al. Multicoil Dixon chemical species separation with an iterative least-squares estimation method. Magn Reson Med 2004:51:35-45.
8. H. Yu, S.B. Reeder, A. Shimakawa, J.H. Brittain, N.J. Pelc. Field map estimation with a region growing scheme for iterative 3-point water-fat decomposition. Magn Reson Med 2005:54:1032-1039.
9. M. Jacob, B.P. Sutton. Algebraic Decomposition of Fat and Water in MRI. Medical Imaging, IEEE Transactions on 2009:28:173-184.